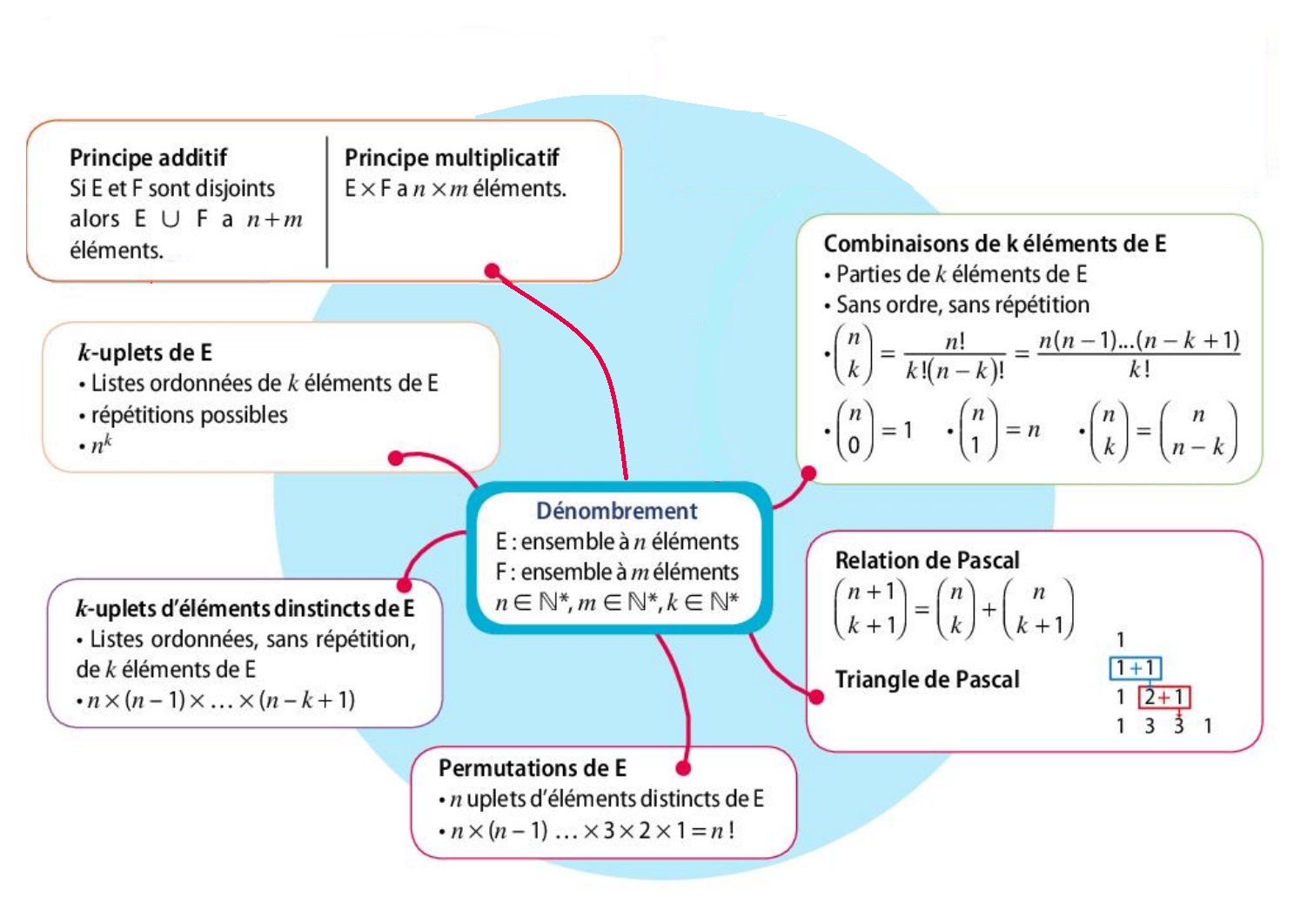
Dénombrement
Dénombrement
Rappel de 2nde
En classe de 2nde, on a appris à dénombrer les issues d'un univers, ce qui revient à compter les éléments d'un ensemble.
Dénombrer les issues avec un tableau
Pour dénombrer les différentes issues dans des expériences aléatoires plus complexes, on pourra utiliser un tableau.
Exemple
On considère l'expérience aléatoire qui consiste à lancer deux dés :
dé 2\dé 1 1 2 3 4 5 6 1 (1 ; 1) (2 ; 1) (3 ; 1) (4 ; 1) (5 ; 1) (6 ; 1) 2 (1 ; 2) (2 ; 2) (3 ; 2) (4 ; 2) (5 ; 2) (6 ; 2) 3 (1 ; 3) (2 ; 3) (3 ; 3) (4 ; 3) (5 ; 3) (6 ; 3) 4 (1 ; 4) (2 ; 4) (3 ; 4) (4 ; 4) (5 ; 4) (6 ; 4) 5 (1 ; 5) (2 ; 5) (3 ; 5) (4 ; 5) (5 ; 5) (6 ; 5) 6 (1 ; 6) (2 ; 6) (3 ; 6) (4 ; 6) (5 ; 6) (6 ; 6) Il y a donc 36 issues possibles.
Dénombrer les issues avec un arbre
Pour dénombrer les différentes issues dans des expériences aléatoires plus complexes, on pourra aussi utiliser un arbre.
Exemple
On considère l'expérience aléatoire qui consiste à tirer successivement Trois jetons dans un sac contenant 4 jetons A, B, C et D :
Il y a donc 24 issues possibles, Ω = {ABC ; ABD ; ACB ; ACD ; ...}.
L'inconvénient des arbres, c'est leur taille. Pour remédier à ce problème, on peut utiliser la méthode des cases qui consiste à marquer à chaque étape dans une case le nombre de choix.
Dans notre exemple il y a 3 cases.

On retrouve le résultat \(4\times 3\times 2 =24\)
Les principes de dénombrement
Principe additif
Exemple
- E={A ; B ; C} alors card(E)=3.
Commentaires
- E={A ; B ; C} et F={V ; W} alors E∪F={A ; B ; C ; V ; W} et évidemment card(E∪F)=5.
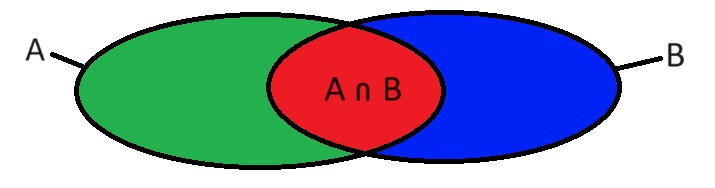
- Si les ensembles ne sont pas disjoints, alors on les découpe pour former une réunion d'ensembles disjoints.
Par exemple :
On découpe en 3 ensembles {les éléments que dans A} ∪ {A∩B} ∪ {les éléments que dans B}.
Principe multiplicatif
Commentaires
- Les éléments peuvent être des nombres, des lettres, des cartes, des fruits, en fait n'importe quoi.
- (1;2) et (A;3) sont deux couples.
- (1;2;3) et (A;3;#) sont deux triplets.
- (1;2;3;4;5;6;G) est un 7-uplets.
Commentaires
Notation : E×E×...×E (il y a k fois E)= Ek.
Si E={A;B} et F={1;2;3}.
- E×F={(A;1);(A;2);(A;3);(B;1);(B;2);(B;3)}.
- F×E={(1;A);(2;A);(3;A);(1;B);(2;B);(3;B)}.
- E×E×E={(A;A;A);(B;A;A);(A;B;A);(A;A;B);(A;B;B);(B;A;B);(B;B;A);(B;B;B)}.
- (1;1;1;1;1;1;1) est un 7-uplets de F7.
Exemples
Si E={A;B} et F={1;2;3}.
- card(E×F)=2×3=6.
- card(E×E×E)=2×2×2=23=8.
- card(F7)=37.
Cas particulier : Nombre des parties d’un ensemble à n éléments
Soit E un ensemble de n éléments et F={0;1}.
Pour dénombrer les parties de E, on remarque que chaque partie A de E peut s'écrire comme un n-uplet composé de 0 et de 1 en respectant la règle suivante si le kième élément de E appartient à A alors la kième valeur du n-uplet sera 1 sinon 0.
Ainsi le nombre des parties de E sera card(Fn)=2n.
Remarque : on peut faire un raisonnement analogue avec un schéma de Bernoulli (cf arbre).
Remarque : L'ensemble vide est toujours une partie de E. Attention à ne pas l'oublier.
Définir les arrangements et les permutations
Exemple
- 2!=2
- 4!=24
- 80!>10118
Commentaires
LES ARRANGEMENTS TIENNENT COMPTE DE L'ORDRE.
Soit E={1;2;3;4;5;6}.
- (1;5) est un arrangement de 2 éléments de E et (5;1) est un autre arrangement de 2 éléments de E.
- (1;5;3;2) est un arrangement de 4 éléments de E.
- (1;5;3;1) n'est pas un arrangement de 4 éléments de E, car il y a 2 fois "1".
Exemples
- Le nombre d'arrangements de 2 éléments d'un ensemble de 11 éléments est 11×10=110.
- Lors de la finale du 100m il y a 8 athlètes au départ, combien y a-t-il de podiums possibles ?
Un podium tient compte de l'ordre d'arrivée, donc le nombre de podiums est le nombre d'arrangements de 3 éléments d'un ensemble de 8 éléments.
soit 8×7×6=336 podiums
Commentaires
LES PERMUTATIONS TIENNENT COMPTE DE L'ORDRE.
Soit E={1;2;3}.
- (1;2;3) est une permutation de E.
- (1;3;2) est une permutation de E.
- (1;3;1) n'est pas une permutation de E, car il y a 2 fois "1".
Exemples
- Le nombre de permutations d'un ensemble de 3 éléments est 3!=6.
- Lors de la finale du 100m il y a 8 athlètes au départ, combien y a-t-il de classements possibles ?
Un classement est une permutation des 8 athlètes, donc le nombre de classements est 8!
Définir les combinaisons
Commentaires
LES COMBINAISONS NE TIENNENT PAS COMPTE DE L'ORDRE.
Soit E={1;2;3;4;5;6}.
- {1;5} est une combinaison de 2 éléments de E et {5;1} est la même combinaison que {1;5}.
- {1;5;3;2} est une combinaison de 4 éléments de E.
- (1;5;3;1) n'est pas une combinaison de 4 éléments de E, car il y a 2 fois "1".
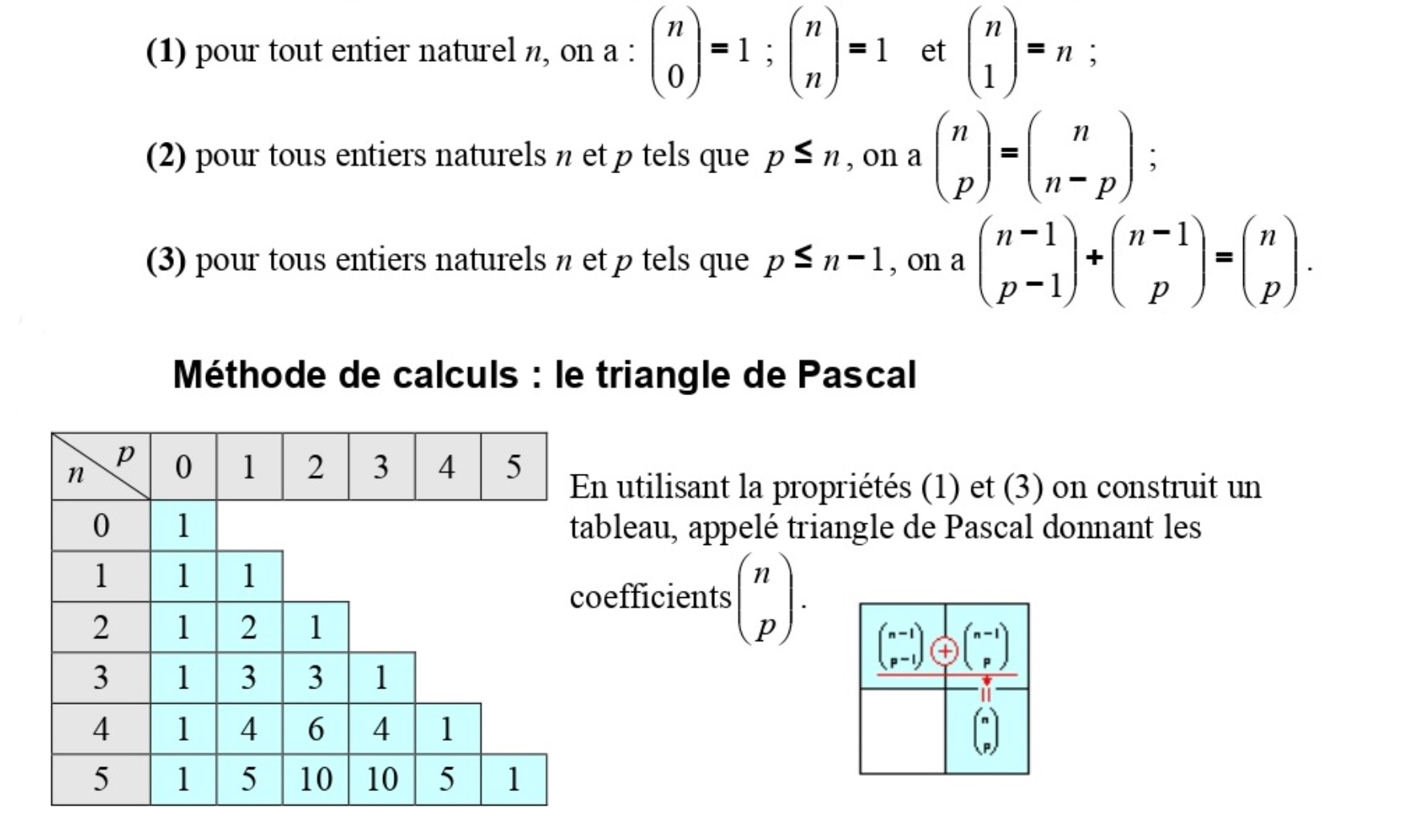
Commentaires
Rappel des propriétés vu avec la loi binomiale.
Bilan : carte mentale