Addition binaire
Objectif
Construire un circuit de portes logiques correspondant à l'addition de deux nombres binaires de 4bits
Les portes logiques : XOR et NON XOR
La fonction XOR
Voici la table de vérité de XOR :
| a |
b |
a $\oplus$ b |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
Ecrire la table de vérité de $s$ = $\bar a$ . $b$ + $a$ . $\bar b$. En complétant le tableau suivant :
| $a$ |
$b$ |
$\bar a$ |
$\bar b$ |
$\bar a$ . $b$ |
$a$ . $\bar b$ |
$s$ |
| 0 |
0 |
|
|
|
|
|
| 0 |
1 |
|
|
|
|
|
| 1 |
0 |
|
|
|
|
|
| 1 |
1 |
|
|
|
|
|
La fonction NON XOR
Ecrire la table de vérité de $\overline {a \oplus b}$.
En déduire que $\overline {a \oplus b}$ = $a$ . $b$ + $\bar a$ . $\bar b$ à l'aide d'une table de vérité.
Principe de l'addition binaire
Voici un exemple d'addition :
0 1 1
1 0 1 1
+ 0 0 1 1
1 1 1 0
Addition des deux bits unitaires
- Combien de possibilités a-t-on avec 2 booléens ( 2 bits).
En déduire le nombre de lignes nécessaires dans une table de vérité avec 2 booléens en entrée.
- Ecrire la table de vérité où en entrée on a 2 booléens a et b (2 bits) et en sortie on a la somme S (voir ci-dessus)
- Ecrire la table de vérité où en entrée on a 2 booléens a et b (2 bits) et en sortie on a la retenue R (voir ci-dessus)
- Construire le circuit ayant 2 entrées (1bit + 1bit) et 2 sorties : la somme S et la retenue R, dans le simulateur
Voir une solution
Addition de deux bits et du bit de la retenue
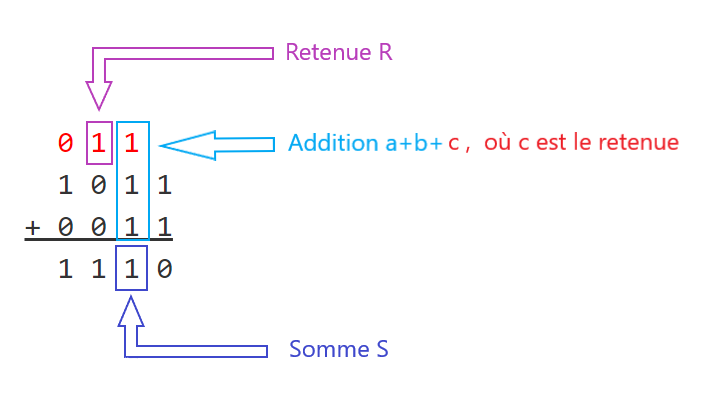
- Combien de possibilités a-t-on avec 3 booléens ( 3 bits).
En déduire le nombre de lignes nécessaires dans une table de vérité avec 2 booléens en entrée.
- Ecrire la table de vérité où en entrée on a 3 booléens a, b et c (3 bits) et en sortie on a la somme S (voir ci-dessus).
On pourra vérifier que S = a $\oplus$ b $\oplus$ c.
- Ecrire la table de vérité où en entrée on a 3 booléens a, b et c (3 bits) et en sortie on a la retenue R (voir ci-dessus)
On pourra vérifier que R = a . b + c.(a $\oplus$ b).
- Construire le circuit ayant 3 entrées (1bit + 1bit + 1bit de la retenue) et 2 sorties : la somme S et la retenue R, dans le simulateur
Voir une solution
Addition de deux nombres binaires de 4 bits
A l'aide des circuits précédents, construire un circuit pour l'addition de deux nombres de 4bits. Donc le circuit aura 2 × 4 booléens en entrées et 5 sorties (4bits +1bit de retenue).
Voir une solution
