
Discriminant
Définition
Commentaire
- La formule du discriminant des polynômes du second degré n'est pas valable pour des fonctions affines ou des polynômes de degré supérieur à 2.
Equation du second degré
Démonstration à connaitre
Commentaire
- IL VAUT MIEUX APPRENDRE CES FORMULES PAR COEUR.
- Lorsque le coefficient \(b\) ou \(c\) est nul, il y a des factorisations évidentes qui permettent une résolution plus rapide.
Factorisation
Démonstration à connaitre
Commentaire
- IL VAUT MIEUX APPRENDRE CES FORMULES PAR COEUR.
- Lorsque le coefficient \(b\) ou \(c\) est nul, il y a des factorisations évidentes.
Signe du trinôme du second degré
Démonstration à connaitre
Interprétation graphique
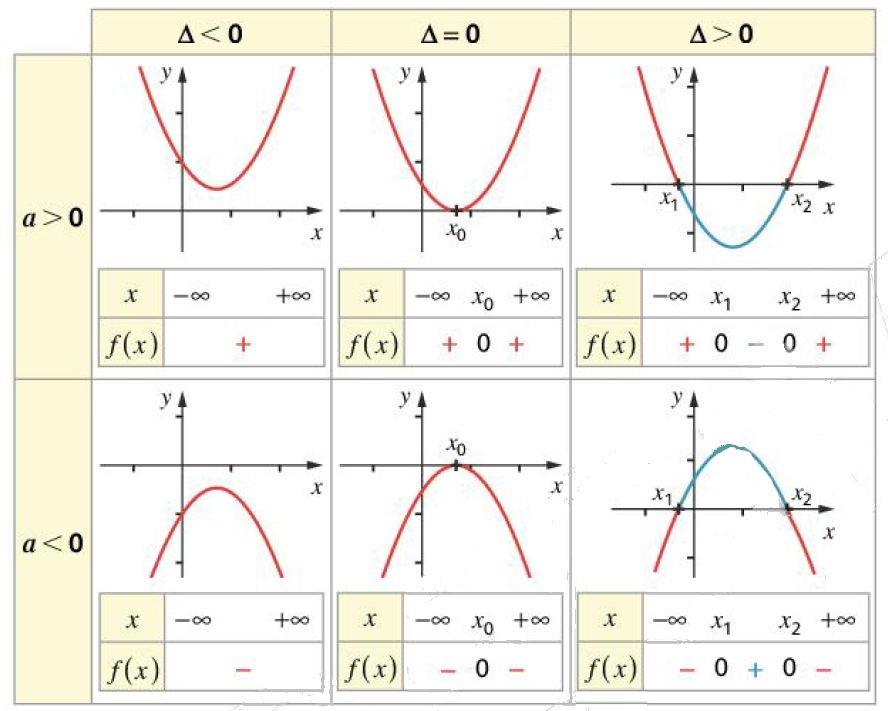
 Discriminant
Discriminant

