On considère une droite (d) et les points A et B situés chacun d'un côté de la droite. La droite (AB) coupe (d) au point O. On note A' et B' les projetés orthogonaux respectifs des points A et B sur la droite (d).
On a les longueurs suivantes : A'B' = 4, AA' = 1 et BB' = 5.
1. Faire une figure en taille réelle.
2. Calculer OA' et OB'.
3. En déduire AB.
Corrigé de l'exercice 11. La figure en taille réelle.
2. Calcul de OA' et OB'.
On note \(x\)=OA'.
Les droites (AA') et (BB') sont parallèles car perpendiculaires à une même troisième (d). Donc les triangles OAA' et OBB' sont en situation de Thalès.
D'après le théorème de Thalès on a : \(\cfrac{OA}{OB}=\cfrac{OA'}{OB'}=\cfrac{AA'}{BB'}\)
D'où \(\cfrac{x}{4-x}=\cfrac{1}{5}\)
Avec le produit en croix : \(5x=4-x\), donc \(x=\cfrac{4}{6}=\cfrac{2}{3}\)
Conclusion : OA'=\(\cfrac{2}{3}\) et OB'=\(4-\cfrac{2}{3}=\cfrac{10}{3}\)
3. Calcul de OA et OB.
On applique le théorème de Pythagore dans le triangle OAA'rectangle en A' :
\(OA^2=A'O^2+A'A^2=\left(\cfrac{2}{3}\right)^2+1^2=\cfrac{13}{9}\) soit \(OA=\cfrac{\sqrt{13}}{3}\)
On applique le théorème de Pythagore dans le triangle OBB'rectangle en B' :
\(OB^2=B'O^2+B'B^2=\left(\cfrac{10}{3}\right)^2+5^2=\cfrac{325}{9}\) soit \(OB=\cfrac{5\sqrt{13}}{3}\)
Conclusion : \(AB=OA+OB=\cfrac{\sqrt{13}}{3}+\cfrac{5\sqrt{13}}{3}=\cfrac{6\sqrt{13}}{3}=2\sqrt{13}\)
Sur la figure ci-contre, A' et B' sont les projetés orthogonaux respectifs de A et de B sur la droite (d).
I est le point d'intersection des droites(AB') et (A'B).
On a : AA' = 2, BB' = 3 et A'B' = 5.
1. Calculer la mesure au degré près de l'angle \(\widehat{AB'A'}\).
2. Calculer la mesure au degré près de l'angle \(\widehat{BA'B'}\).
3. Calculer la mesure au degré près de l'angle \(\widehat{AIB}\).
Corrigé de l'exercice 21. Dans le triangle AA'B' rectangle en A', on a : \(tan(\widehat{AB'A'})=\cfrac{AA'}{A'B'}\).
\(tan(\widehat{AB'A'})=\cfrac{2}{5}\). Avec la calculatrice \(\widehat{AB'A'}=22°\)
2. Dans le triangle BA'B' rectangle en B', on a : \(tan(\widehat{BA'B'})=\cfrac{BB'}{A'B'}\).
\(tan(\widehat{BA'B'})=\cfrac{3}{5}\). Avec la calculatrice \(\widehat{BA'B'}=31°\)
3. Dans le triangle IA'B', on a : \(\widehat{IA'B'}+\widehat{IB'A'}+\widehat{A'IB'}=180°\).
Ou encore \(\widehat{BA'B'}+\widehat{AB'A'}+\widehat{A'IB'}=180°\)
En remplaçant : \(31°+22°+\widehat{A'IB'}=180°\)
\(\widehat{A'IB'}=180°-(31°+22°)=127°\)
Les angles \(\widehat{A'IB'}\) et \(\widehat{AIB}\) sont opposés par le sommet donc de même mesure.
Conclusion : \(\widehat{AIB}=127°\)
On considère un triangle ABC isocèle en A tel que :
1. Justifier que le point H est le milieu de[BC].
2. Justifier que le demi-cercle C ne coupe qu'une seule fois le côté [AC], en I.
3. Calculer la valeur exacte de la longueur AH.
4. Calculer la valeur exacte de la longueur HI.
5. En déduire la valeur exacte de l'aire du demi-disque (partie en rouge sur la figure).
Corrigé de l'exercice 31. H est le projeté orthogonal de A sur [BC], donc H est le point de (BC) tel que (AH) perpendiculaire à (BC). Donc (AH° est la hauteur issue de A de ce triangle.
Dans un triangle isocèle en A, donc sa hauteur issue de A est aussi une médiane, donc H est le milieu de [BC].
2. Le rayon [IH] est perpendiculaire à (AC) donc (AC) est une tangente de ce cercle. Donc I est l'unique point d'intersection entre le demi-cercle C et (AC).
3. D'après le théorème de Pythagore dans le triangle ABH rectangle en H :
\(AB^2=AH^2+HB^2\) donc \(4^2=AH^2+3^2\) donc \(AH^2=16-9=7\) donc \(AH=\sqrt{7}\)
4. L'aire du triangle ACH est la moitié de l'aire du triangle ABC.
AireACH=\(\cfrac{B\times h}{2}=\cfrac{AC\times HI}{2}=2HI\)
AireABC=\(\cfrac{B\times h}{2}=\cfrac{BC\times AH}{2}=3\sqrt{7}\)
AireABC=2×AireACH, donc \(2\times 2HI=3\sqrt{7}\) donc \(HI=\cfrac{3\sqrt{7}}{4}\)
5. L'aire d'un demi-disque : \(Aire=\cfrac{\pi r^2}{2}=\cfrac{\pi \times \left(\cfrac{3\sqrt{7}}{4}\right)^2}{2}=\cfrac{63}{32}\pi\)
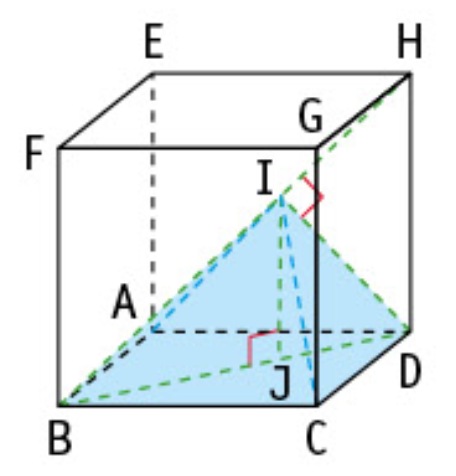
ABCDEFGH est un cube d'arêtes de longueur 3 cm. En considérant le triangle BDH rectangle en D.
On note I le projeté orthogonal du point D sur la droite (BH).
On note J le projeté orthogonal du point I sur la droite (BD).
Le but de cet exercice est de calculer le volume de la pyramide ABCDI de base carrée ABCD et de hauteur IJ.
1. Calculer la longueur BD.
2. Tracer le triangle BDH rectangle en D. Placer les points I et J.
3. Calculer la longueur BH.
4. Calculer la longueur BI.
5. En déduire la longueur IJ.
6. Calculer le volume de la pyramide ABCDI.
Corrigé de l'exercice 41. D'après le théorème de Pythagore dans le triangle ABD rectangle en A, on a :\(BD^2=AB^2+AD^2=3^2+3^2=18\)
Donc \(BD=\sqrt{18}=3\sqrt{2}\).
2. La figure :
3. D'après le théorème de Pythagore dans le triangle BDH rectangle en D, on a :\(BH^2=DH^2+BD^2=3^2+18=27\)
Donc \(BH=\sqrt{27}=3\sqrt{3}\).
4. Dans le triangle BDH rectangle en D, on a :\(cos(\hat{B})=\cfrac{BD}{BH}\).
Dans le triangle BDI rectangle en I, on a :\(cos(\hat{B})=\cfrac{BI}{BD}\).
Donc \(BI=BD\times cos(\hat{B})=\cfrac{BD\times BD}{BH}=\cfrac{18}{3\sqrt{3}}=2\sqrt{3}\)
5. Les droites (HD) et (IJ) sont perpendiculaires à (BD), donc elles sont parallèles.
Les triangles BIJ et BDH sont en situation de Thalès, donc d'après le théorème de Thalès : \(\cfrac{BI}{BH}=\cfrac{IJ}{HD}\).
Donc \(IJ=\cfrac{BI\times HD}{BH}=\cfrac{2\sqrt{3}\times 3}{3\sqrt{3}}=2\)
6. La formule du volume d'une pyramide : \(V=\cfrac{B\times h}{3}\).
Donc \(V=\cfrac{B\times h}{3}=\cfrac{Aire(ABCD)\times IJ}{3}=\cfrac{3^2\times 2}{3}=6\).
Conclusion : Le volume de la pyramide ABCDI est 6 cm3.
On considère le triangle ABC rectangle en B tel que AB = 5 et BC = 3. On place un point M sur le segment [AB] et on note \(x\) la longueur AM.
On appelle D le point d'intersection de la droite (AC) avec la perpendiculaire à (AB) passant par M et E le quatrième sommet du rectangle BMDE.
L'objectif de cet exercice est de déterminer la position de M qui rend l'aire de BMDE maximale.
1. Quelles sont les valeurs possibles pour \(x\) ?
2. Exprimer la longueur BM, puis la longueur DM en fonction de \(x\).
3. Exprimer l'aire A(\(x\)) du rectangle BMDE en fonction de \(x\).
4. Monter que A(\(x)=-0,6(x-2,5)^2+3,75\).
5. En déduire pour quelle valeur de \(x\) l'aire de BMDE est maximale, et quelle est cette aire.
Corrigé de l'exercice 51. \(x\) prend ses valeurs entre 0 et 5.
2. Expression en fonction de \(x\)
3. La formule de l'aire d'un rectangle : A= L×l.
A(\(c\)) = BM×MD = \((5-x)\times\cfrac{3x}{5} = 3x -0,6x^2\).
4. On développe \(-0,6(x-2,5)^2+3,75\)
\(-0,6(x-2,5)^2+3,75=-0,6(x^2-5x+6,25)+3,75\).
\(-0,6(x-2,5)^2+3,75=-0,6x^2+3x-3,75+3,75\)
\(-0,6(x-2,5)^2+3,75=-0,6x^2+3x=\)A(\(x\))
5. \((x-2,5)^2\geqslant 0\) car un carré est toujouts positif.
\(-0,6\times (x-2,5)^2\leqslant -0,6\times 0\) l'ordre change car on multiplie par un nombre négatif
\(-0,6(x-2,5)^2 +3,75\leqslant 3,75\) on ajoute 3,75 de chaque côté.
On remarque que A(\(2,5\))\(=3,75\).
Donc A(\(x\))\(\leqslant \) A(\(2,5\))
On en déduit que A atteint son maximum en 2,5 et vaut 3,75.