Généralités

Définition et vocabulaire

Définitions

Soit D un intervalle ou une réunion d'intervalles de ℝ.
On appelle fonction à valeurs réelles f définie sur D un procédé qui à tout réel x de D associe un unique réel noté f(x).
D est appelé l'ensemble de définition de la fonction f.
Pour un nombre a de D, si f(a)=b, on dit que :

b est l'image de a par la fonction f.
a est l'antécédent de b par la fonction f.

Commentaires

L'image de a est unique.
Il se peut que b ait 0, 1 ou même plusieurs antécédents.

b = 1

Représentation graphique d'une fonction

Définitions

Dans un repère du plan, on appelle courbe représentative ou représentation graphique de la fonction f, notée C_f l'ensemble des points M de coordonnées (x ; y) qui vérifient :

x∈D et y = f(x).
La relation y = f(x) est appelée équation de la courbe C_f.

Avec la numworks

Avec la

Parité d'une fonction

Définition

On considère une fonction f définie sur l'ensemble D.
On dit que f est paire si :

D est centré en 0.
pour tout réel x de D, on a f(-x)=f(x).

Propriété

On considère une fonction f définie sur l'ensemble D.
Si f est paire, alors sa courbe représentative C_f est symétrique par rapport à l'axe des ordonnées.

Exemple

x = 2.0

Définition

On considère une fonction f définie sur l'ensemble D.
On dit que f est impaire si :

D est centré en 0.
pour tout réel x de D, on a f(-x)=-f(x).

Propriété

On considère une fonction f définie sur l'ensemble D.
Si f est impaire, alors sa courbe représentative C_f est symétrique par rapport à O l'origine du repère.

Exemple

x = 4.0

Résolution graphique d'équations et d'inéquations

Théorème

Soit C_f la courbe représentative d'une fonction f définie sur un ensemble D dans un repère donné.
Pour tout réel k, les solutions dans D de l'équation f(x)=k sont les abscisses des points d'intersection de C_f et de la droite d'équation y=k.

Théorème

Soit C_f la courbe représentative d'une fonction f définie sur un ensemble D dans un repère donné.
Pour tout réel k, les solutions dans D de l'inéquation f(x)<k sont les abscisses des points de C_f situés strictement en dessous de la droite d'équation y=k.

Exemple

k = 1

Théorème

Soient C_f et C_g les courbes représentatives de deux fonctions f et g dans un même repère.
Les solutions de l'équation f(x)=g(x) sont les abscisses des points d'intersection de C_f et C_g.

Théorème

Soient C_f et C_g les courbes représentatives de deux fonctions f et g dans un même repère.
Les solutions de l'inéquation f(x)<g(x) sont les abscisses des points de C_f situés strictement en dessous de C_g.

Variations et extremums d'une fonction

Définition

La fonction f est strictement croissante sur un intervalle I lorsque pour tous nombres a et b de I :

si a<b, alors f(a)<f(b).

Définition

La fonction f est strictement décroissante sur un intervalle I lorsque pour tous nombres a et b de I :

si a<b, alors f(a)>f(b).

Définition

La fonction f est strictement constante sur un intervalle I lorsque pour tous nombres a et b de I :

si a<b, alors f(a)=f(b).

Commentaires

Etudier les variations d'une fonction revient à rechercher les intervalles sur lesquels la fonction est croissante ou décroissante. On résume les variations d'une fonction dans un tableau de variation avec les règles suivantes :

Si la fonction est croissante, on utilise une flèche qui monte ;
Si la fonction est décroissante, on utilise une flèche qui descend ;
Si la fonction est constante, on utilise une flèche horizontale ;
A chaque extrémité des flèches, on met les valeurs correspondantes de la fonction.

Définitions

Soit f une fonction définie sur un intervalle I et soit a un réel de l'intervalle I. On dit que :

f admet un maximum en a sur I lorsque, pour tout x∈I, f(x)≤f(a) ;
f admet un minimum en a sur I lorsque, pour tout x∈I, f(x)≥f(a) ;
f admet un extremum en a sur I, si f admet un minimum ou un maximum en a sur I.

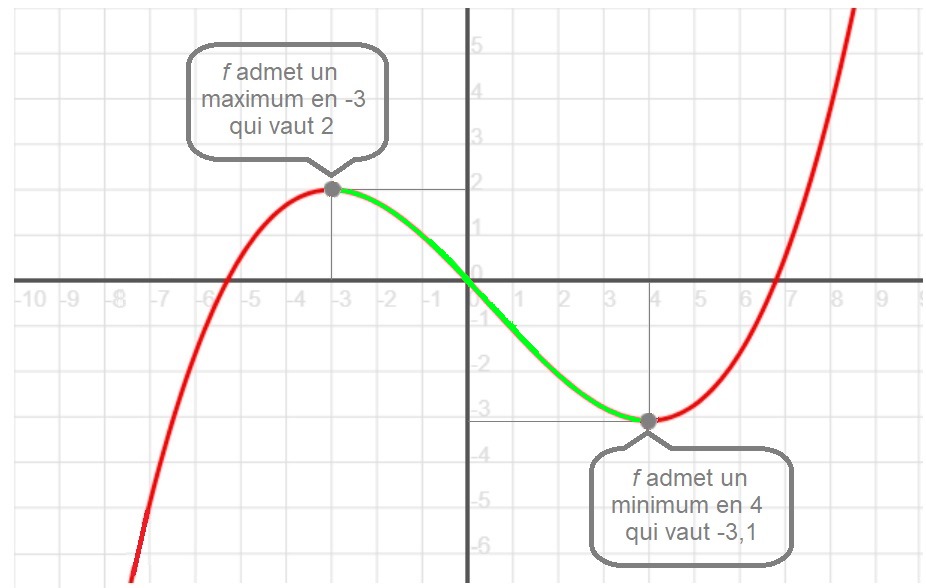
Exemple

Le tableau de variations

x -7,5 -3 4 8,5

f(x) -7 2 -3,1 6

Les extremums

Cette fonction admet un maximum en -3 sur [-7;0]

Cette fonction admet un minimum en 4 sur [0;8]

x	-7,5		-3		4		8,5
f(x)	-7		2		-3,1		6

Variation des fonctions affines

Définition

Soit \(f\) une fonction définie sur un intervalle I, et soient \(a\) et \(b\) deux réels de l'intervalle I tels que \(a\lt b\). On appelle taux d'accroissement de \(f\) entre \(a\) et \(b\) le nombre \(t\) défini par :

\(t=\cfrac{f(b)-f(a)}{b-a}\)

Commentaires

Si pour tous réels \(a\) et \(b\) de l'intervalle I, t est positif, alors \(f\) est croissante sur I.
Si pour tous réels \(a\) et \(b\) de l'intervalle I, t est négatif, alors \(f\) est décroissante sur I.

Propriétés

Soient m et p deux réels et f la fonction affine définie par f(x)=mx+p sur ℝ.
Le taux d'accroissement de f entre \(a\) et \(b\) est égal à m le coefficient directeur.
D'où les conséquences :

Si m est positif, alors f est croissante sur ℝ.
Si m est négatif, alors f est décroissante sur ℝ.
Si m est égal à 0, alors f est constante sur ℝ.

Démonstration

Soient \(a\) et \(b\) deux réel tels que \(a\lt b\).
\(t=\cfrac{f(b)-f(a)}{b-a}=\cfrac{(mb+p)-(ma+p)}{b-a}=\cfrac{mb-ma}{b-a}=\cfrac{m(b-a)}{b-a}=m \text{, car }b-a\neq 0\)