 Les réels
Les réels
La droite graduée
abscisse : 5
Les ensembles de nombres
Commentaires
- Tous les entiers naturels et relatifs sont des nombres décimaux, mais la réciproque est fausse.
- Tous les nombres décimaux sont des nombres rationnels, mais la réciproque est fausse.
Exemple : 7,11 peut s'écrire \(\frac{711}{100}\).
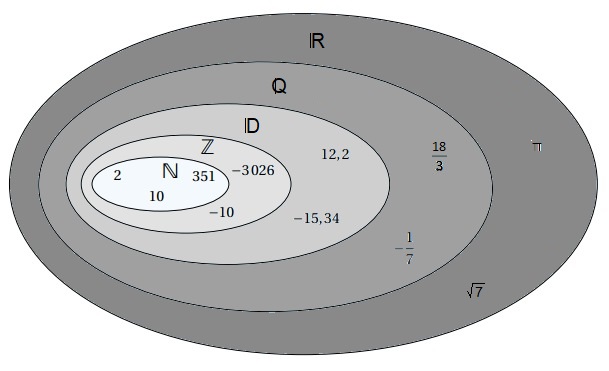
Commentaires
- \(\frac{1}{3}\) ∉ 𝔻. Voir la démonstration dans le chapitre Les ensembles 𝔻 et ℚ .
- \(\sqrt{2}\) ∉ ℚ. Voir la démonstration dans le chapitre Les ensembles 𝔻 et ℚ .
Les intervalles de ℝ
Exemples d'intervalles

Commentaires
- dans l'intervalle [a;b], a est toujours strictement inférieur à b.
- S'il y a ±∞ dans un intervalle, alors le crochet sera ouvert du coté de l'∞.
Commentaires
- Pour trouver I ∩ J, on peut utiliser la droite graduée pour visualiser la réponse.
- De même, I ∪ J.
La valeur absolue
Commentaires
Par exemples :
- |356438| = 356438.
- |-8243| = 8243.
Avec la numworks
Avec la
Commentaires
Par exemples :
- x ∈ [8 ; 12] est équivalent à |x-10| ≤ 2.
- x ∈ ]8 ; 12[ est équivalent à |x-10| < 2.


