Objectif : Découvrir des algorithmes qui permettent :
Le compte est bon est un jeu de calcul où on tire au hasard un nombre puis une série de 6 nombres à partir desquels on doit le premier nombre en utilisant uniquement les 4 opérations +, ×, / et -. Le gagnant est celui qui la réponse la plus proche.
L'idée pour résoudre ce casse-tête est très simple. On énumère toutes les résultats possibles et on choisit le meilleur !
On note LA liste des nombres choisis pour trouver le résultat.
On appelle candidat le nombre le plus proche du résultat.
On rajoute la liste dans la file d'attente A faire.
On affiche la valeur de candidat.
Remarque : pour faire tourner ce type d'algorithme il est conseillé d'utiliser un arbre.
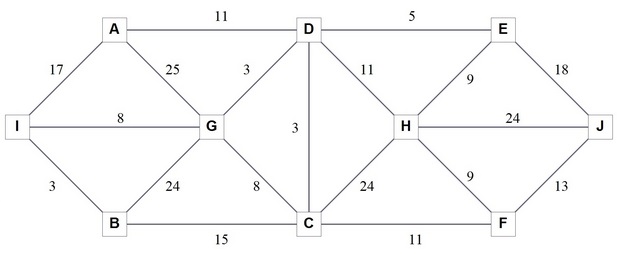
Voici un arbre pour 3 nombres et 2 opérations + et ×.
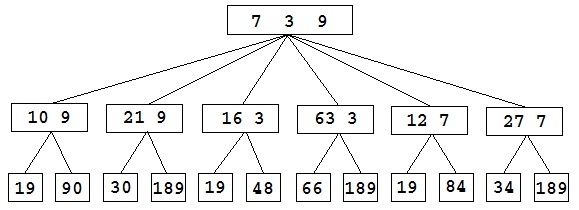
Voir le projet : IA avec le compte est bon
Pour simplifier l'exercice, on doit le résultat à partir de seulement 4 nombres et on n'utilise que les 2 opérations + et ×.
Trouver le meilleur résultat pour obtenir 402 avec 3 - 3 - 10 - 25.
L'application aux jeux a toujours été un domaine actif de l'Intelligence Artificielle. On s'intéresse ici au jeu du morpion opposant deux joueurs (chacun joue à son tour), à information complète (chacun sait tout de la situation de jeu, à chaque instant).
Dans la suite, on note J1 et IA les deux joueurs et l'on se place dans la situation c'est à AI de jouer.
Le déroulement de la partie peut être vu comme un arbre :
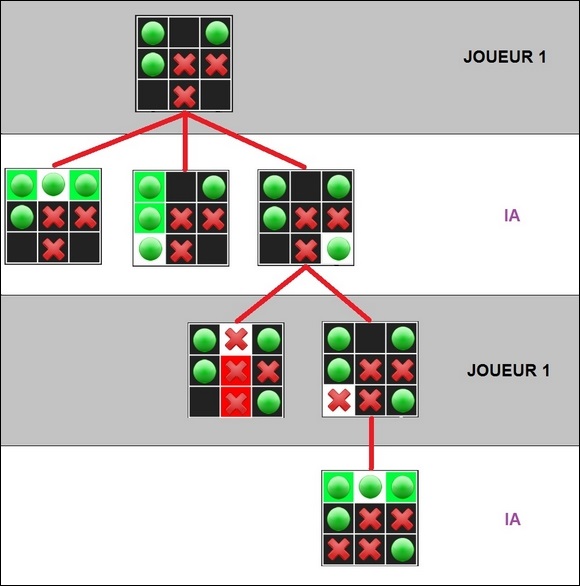
Une fois arbre élaboré, l'IA va chercher le meilleur coup avec l'algorithme min-max.
On prend la convention suivante :
L'idée est de l'algorithme est de développer complètement l'arbre de jeu, de noter chaque feuille avec sa valeur, puis de faire remonter ces valeurs avec l'hypothèse que chaque joueur choisit le meilleur coup pour lui. Cela signifie en pratique que :
Remarque : ce type d'algorithme se programme utilise la récursivité.
Voir le projet : Morpion avec IA

Le graphe ci-dessous indique les distances entre les différents points. On veut relier les points E et S par le chemin le plus court.
L'algorithme de Dijkstra est basé sur le principe suivant :
Si le plus court chemin reliant E à S passe par les sommets , , …, alors, les différentes étapes sont aussi les plus courts chemins reliant E aux différents sommets , , …, .
On construit de proche en proche le chemin cherché en choisissant à chaque itération de l'algorithme, un sommet du graphe parmi ceux qui n'ont pas encore été traités, tel que la longueur connue provisoirement du plus court chemin allant de E à soit la plus courte possible.
Étape 1 : On affecte le poids 0 au sommet origine (E) et on attribue provisoirement un poids ∞ aux autres sommets.
Étape 2 : Parmi les sommets dont le poids n'est pas définivement fixé choisir le sommet X de poids p minimal. Marquer définitivement ce sommet X affecté du poids p(X).
Étape 3 : Pour tous les sommets Y qui ne sont pas définitivement marqués, adjacents au dernier sommet fixé X :
Le plus court chemin de E à S s'obtient en écrivant de gauche à droite le parcours en partant de la fin S.
Vous pouvez observer le déroulement de l'algorithme de Dijkstra pas à pas en cliquant sur les boutons
Pour faciliter la recherche du plus court chemin il est commode de présenter les résultats dans un tableau
| E | A | B | C | D | F | G | S | Sommet sélectionné et commentaires |
| 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | E de poids 0 on marque les sommets adjacents A, B et C |
| 5 (E) | 3 (E) | 2(E) | ∞ | ∞ | ∞ | ∞ | C on selectionne les sommets adjacents G et F, on les marque provisoirement G(2+3) et F(2+2) |
|
| 5 (E) | 3 (E) | ∞ | 4 (C) | 5 (C) | ∞ | B le sommet adjacent A est affecté d'un poids égal à 4 (3+1<5) |
||
| 4 (B) | ∞ | 4 (C) | 5 (C) | ∞ | A le sommet D va être marqué provisoirement avec un poids 6= 4+2 |
|||
| 6 (A) | 4 (C) | 5 (C) | ∞ | F le sommet adjacent D sera affecté d'un poids égal à 5 (4+1<6) le sommet S va être marqué provisoirement avec un poids 10= 4+6 |
||||
| 5(F) | 5 (C) | 10 (F) | D on conservera le poids de S (5+7>10 ) |
|||||
| 5 (C) | 10 (F) | G le sommet adjacent est déjà traité |
||||||
| 10 (F) | S |
Pour déterminer le trajet le plus court on remonte les sommets en partant de S : S vient de F qui vient de C qui vient de E.
Le plus court chemin est E-C-F-S, la distance parcourue est de 10 km.
Voir le projet : Les graphes avec kineticJS
A partir du graphe ci-dessous, dresser le tableau qui permet de trouver le plus court chemin reliant I à J.